Bliźniaki
Są łamigłówki, które łatwiej rowiązywać niż jasno i zwięźle opisać, o co w nich chodzi. Początkowo wydawało mi się, że tak właśnie jest w przypadku poniższych bliźniaków, które sporadycznie pojawiają się w prasie japońskiej. Z czasem doszedłem do wniosku, że chyba trochę przesadziłem.
Diagram jest kwadratowym układem białych pól (kółka) i łączących je dróg. W części pól są liczby. Zadanie polega na wpisaniu jakichś liczb do niektórych pozostałych pól. Są dwa podstawowe warunki dotyczące wartości i rozmieszczenia wszystkich liczb:
a) każda liczba X powinna występować w diagramie parzystą liczbę razy (2, 4, 6,… rzadko więcej), a wszystkie liczby X powinny tworzyć pary bliźniacze;
b) bliźniaczość pary oznacza, że najkrótsza droga od jednej liczby do drugiej przechodzi przez liczbę pustych pól równą wartości tych liczb (zera na sąsiednich polach, jedno pole między jedynkami, dwa miedzy dwójkami itd.).
Jeśli liczb X jest więcej niż dwie, czyli tworzą one przynajmniej dwie pary bliźniacze, to pary te powinny być od siebie całkowicie odizolowane, czyli nie może być drogi łączącej liczbę X w jednych bliźniakach z liczbą X w innych.
Poniżej z lewej strony przykład, z prawej zadanie (raczej twardy orzech).
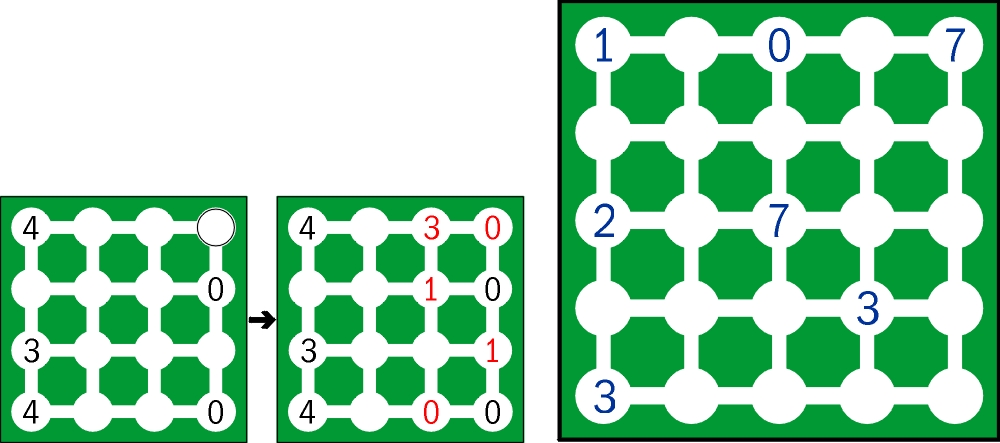
Sposób podania rozwiązania, np. tak (przykładu): 4P30/PP10/3PP1/4P00, gdzie P oznacza puste pole.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Rozwiązałem dość szybko ale nie było łatwo.
Kapitalna łamigłówka.
Aż chce się zakrzyknąć: „prosimy o więcej !”.
Nie wiem czy to jedyne rozwiązanie, ale mam takie:
10017/P19PP/2971P/PPP3P/32PPP
1 0 0 P 7
P 1 P 0 P
2 P 7 0 P
P P P 3 P
3 2 P P P
Uwaga jak do Antypa
mp
100P7/P1P0P/2P70P/PPP3P/32PPP
Wydaje mi się, że w opisie zadania zabrakło jednego warunku. Bez niego zadanie staje się trywialnie proste. Dodanie tego warunku czyniłoby zadanie zdecydowanie trudniejszym, ale też dającym (chyba) tylko jedną odpowiedź. Oto, co proponuję, jako uzupełnienie opisu:
Poszczególne drogi pomiędzy parami liczb powinny tworzyć taki ciąg, w którym przejście do następnego etapu (do kolejnej pary) jest możliwe, jeśli liczba końcowa pary poprzedzającej sąsiaduje z liczbą początkową pary następującej po niej.
Tak jest w zadaniu przykładowym. Kolejne pary to 4-4, 3-3, 0-0, 1-1, 0-0.
Moim zdaniem taki warunek dodatkowy jest zbędny. Alem ciekaw, co o tym sądzą inni komentatorzy.
mp
Poprzedni wpis zawiera błąd i proszę o usunięcie go.
10017
P19PP
2971P
PPP3P
32PPP
Warunek podany przez grgkh spowodowałby chyba katorgę dla układającego zadanie. Ale potwierdzam, że zadanie jest bardzo łatwe. Chyba, że czegoś nie zrozumiałem. A oto rozwiązanie:
1×007
x1xxx
2x7xx
xxx3x
32xxx
100P7/P1P0P/2P70P/PPP3P/32PPP. Są dwie drogi łączące 2. Ale to nie jest zabronione ?
Ale zabronione jest, aby był kontakt (pusta droga) między cyframi z różnych par, a tu tak jest w przypadku zer.
mp
Zadanie grgkh:
Trochę trudniej się robi.
1 0 0 1 7
P 1 9 P P
2 9 7 1 P
P P P 3 P
3 2 P P P
Odniosę się do kwestii sugerowanej przez @grgkh „trywialności” tego gatunku łamigłówki.
W linku zamieściłem zadanie, które stworzyłem korzystając z przepięknych plansz stworzonych przez Naszego Gospodarza.
Sądzę, że nie jest ono trywialne (a ciągle poruszamy się tu na planszy o niezbyt wybujałym rozmiarze).
https://zapodaj.net/plik-8jzsicVQsO
Nie chciałem w poprzednim, opublikowanym wpisie ujawniać rozwiązania, ale jeśliby pominąć warunek ciągłości trasy, to zadanie ma jeszcze drugie rozwiązanie, moim zdaniem mniej eleganckie, pozostawiające więcej niezajętych pól.
W tym przypadku nie da się ustalić trasy będącej nieprzerwanym ciągiem, od pary do pary.
Nie wiem, jak ten typ łamigłówek był przedstawiany w innych, oryginalnych zadaniach tego typu.
Źle, bo od jedynki z jednej pary można dojść białymi drogami i pustymi polami do jedynki z drugiej pary (a nawet do obu drugich jedynek)
mp
Uwaga techniczna dotycząca mojego zadania z linka:
Przed rozwiązywaniem na planszy należy dopisać liczbę 7 (siedem) w polu D1 (notacja szachowa).
(czyli jest to pole czwarte od lewej w wierszu pierwszym od dołu).
10017
P19PP
2971P
PPP3P
32PPP
Poprzednio zignorowałem jeden warunek zadania
Zadanko Apratado:
7 P 0 5 P 0
P P 0 P 1 0
4 P P P P 1
1 3 P 2 P P
P 4 P P P 2
1 3 P 7 5 P
10017/P19PP/2971P/PPP3P/32PPP. Kluczowe jest odcięcie najkrótszych dróg (o długości 3) między 7.
@apartado
Po dopisaniu liczby 7 w polu D1 nadal nie ma jednoznaczności rozwiązania.
@Andrzej111
Co gorsza nie ma go też kiedy umieścimy tę siódemkę na A6.
Może pomoże umieszczenie w OBU tych miejscach ? – któż to wie…
To jest konstrukcja „na szybko”- eksplorująca /eksponująca element brakujący – bez silenia się na Nobla w konstrukcji łamigłówek (zresztą chyba takiego nie ma).
@apartado
@Andrzej111
Jednoznaczne rozwiązanie determinuje umieszczenie dwóch ujawnionych szóstek w B6 i D1. Ich ścieżka blokuje kolumny B i C dla innych wpisów, a tego potrzeba dla czwórki z B2 i stowarzyszonej z nią drugiej, możliwej do wstawienia jedynie na A4.
Zablokowanie zer z prawego górnego narożnika innymi liczbami niż jedynki też musiałoby prowadzić do niejednoznaczności, gdyż E4 daje jednoczesny dostęp do dwóch (wtedy koniecznie różnych od siebie, ale jakich) liczb, np. 4 i 6. Niemożliwe jest też alternatywne (dla blokady zer jedynkami) jednoczesne blokowanie pól D2 i D4, bo w arsenale do wykorzystania mamy tylko 4 i 6, a obie one wymagałyby wstawienia drugich końców w najbardziej oddalonym polu a6.
Taka analiza związana z poszukiwaniem jednoznaczności to spory plus tego pomysłu apartado , bo samo rozwiązywanie zadania po dopisaniu tych szóstek wydaje się stosunkowo łatwe.
___
@mp
W rzeczy samej :), moje niedopatrzenie. Nie zrozumiałem do końca drugiego warunku zadania. Wydało mi się, że jeśli od jakiejś liczby można znaleźć najkrótszą drogę do dowolnej innej, mogącej stanowić dla niej parę, to to determinuje ten związek z ignorowaniem alternatywy. Nieuwaga czytania, to mi się nieraz już tutaj zdarzało.
A czy nie byłoby ciekawym wariantem dla takiego zadania ustalenie warunków, tak jak je tu powyżej formułowałem, z porzuceniem całkowitej izolacji par, które narzuca najkrótsza możliwa droga łącząca, ale z przymusem tworzenia jednego ciągu wszystkich przylegających do siebie końcami par? Może znajdę kiedyś czas, by taką strategię rozważyć i zaproponuję jakieś oparte na niej zadanie…
Na razie wciągnęło mnie układanie zadań na warunkach podanych na wstępie. Mam już coś do zaproponowania, ale powstrzymam się od publikowania i podeślę propozycje do oceny Gospodarzowi, może coś nadałoby się do zaproponowania gronu czytelników Łamibloga.