Siedmiokącik

5 lipca 2025
Marek Penszko

Diagram z lewej strony przedstawia 7-kąt, którego wierzchołki leżą w węzłach siatki kwadratowej (to warunek Q), a długości boków są kolejnymi liczbami naturalnymi od 1 do 7 (to warunek V); jednostką jest oczywiście odległość między węzłami w rzędzie.

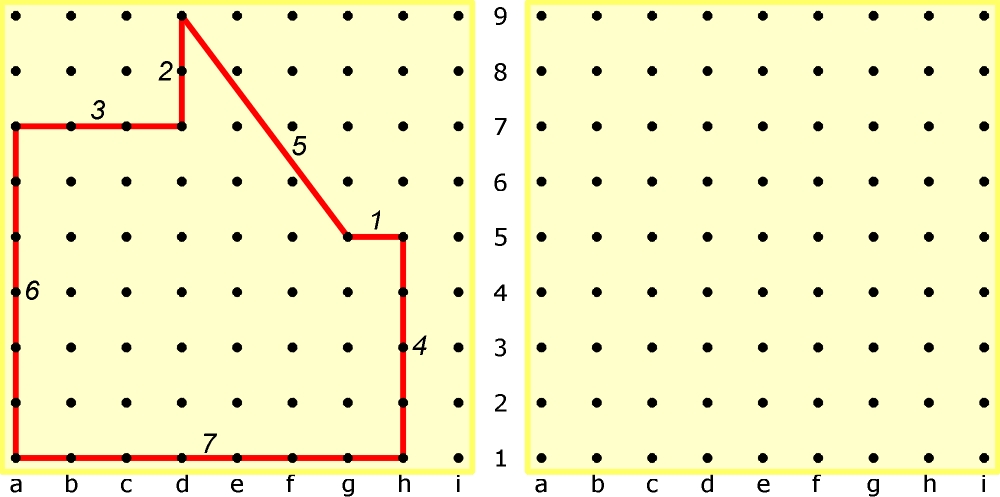
Powierzchnia tego siedmiokąta wynosi 40.
Zadanie polega na wrysowaniu w taką samą siatkę (diagram z prawej) siedmiokąta spełniającego warunki Q i V, ale takiego, którego powierzchnia będzie najmniejszą możliwą. W rozwiązaniu można podać współrzędne siedmiu kątów (zapisem przykładowej 40-ki jest: a1-h1-h5-g5-d9-d7-a7). Podanie samej powierzchni nie wystarczy.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Reklama