9 kapsułek
Duża grupa diagramowych zadań logicznych polega na ustalaniu rozmieszczenia elementów w oparciu o kojarzące się z prostokątnym układem współrzędnych widoki tego rozmieszczenia z dwóch stron. Za pierwowzór takich zadań uchodzi gra w okręty w wersji łamigłówkowej, która debiutowała na łamach argentyńskiego magazynu „Humor & Juegos” w 1982 r. W trywialnym i abstrakcyjnym (geometria zamiast statków) poniższym miniprzykładzie należy zaczernić 6 kratek, tworzących trzy nie stykające się (także rogami) prostokąty: 1×1, 1×2 i 1×3. Liczba przy brzegu oznacza, ile kratek powinno być zaczernionych w danym rzędzie.
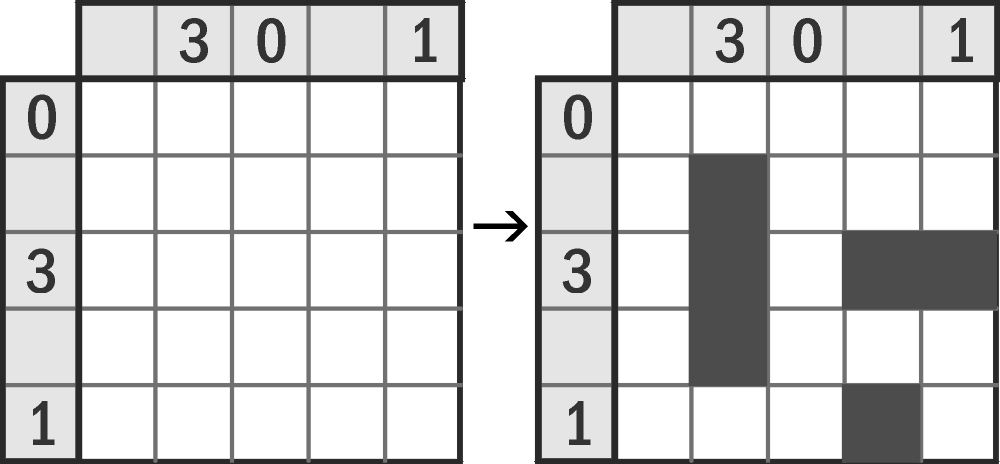
Gdy flotę ograniczono do trójmasztowców i przypisano im wartości, pojawiły się kapsułki, których rozmieszczenie jest ujawnione, a zadanie polega na przypisaniu każdej kapsułce innej wartości z określonego zakresu: w przykładzie – od 1 do 4, w zadaniu – od 1 do 9. Liczba przy brzegu jest sumą wartości kapsułek, które w całości lub w jednej trzeciej występują w danym rzędzie.
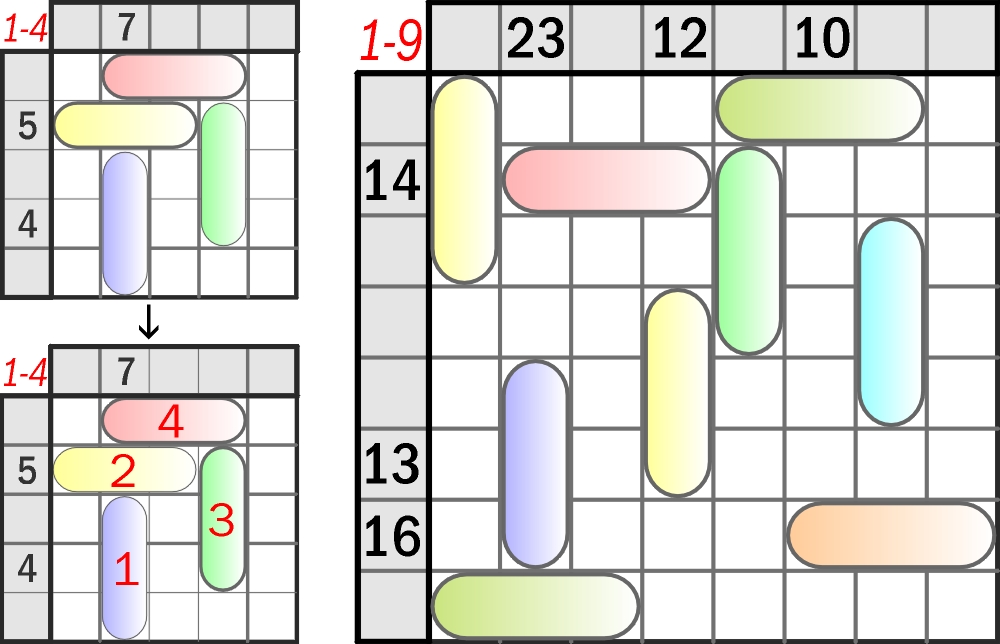
Pytanie końcowe: którą dwucyfrową liczbę należy dopisać przy lewym brzegu diagramu – i w której szarej kratce – aby było tylko jedno rozwiązanie?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Rozwiązując w pamięci, 11=4+5+2, umieszczone w środku pomiędzy 14 i 13, w piątym wierszu od dołu licząc
To zadanie trochę przypomina sposobem analizy kakuro. Doświadczeni tamtymi przykładami mają tu łatwiej.
Bez dodatkowego warunku są dwa rozwiązania. Jedno rozwiązanie otrzymamy wpisując w czwartym wierszu od góry sumę 11.
https://zapodaj.net/plik-ILnyLEcV7v
11 w wierszu nr 4.
Wyglądało groźnie ale okazało się przyjemną dystrakcją w oczekiwaniu na finał Wimbledonu.
Czwarte pole od góry zawiera 11.
Od lewego górnego rogu mamy wtedy: 1, 3, 8, 5, 2, 4, 9, 7, 6.
1,3,8,5,2,4,9,7,6; Liczba to 11 czwarta od góry.
Z kapsułkami trzeba ostrożnie. Zaczynamy od 1, a po sprawdzeniu co z tego wyniknie, możemy łyknąć dwie, a nawet trzy.
a5=11