Słupek

Od czasu do czasu pozwalam sobie na przechwałki, zamieszczając moje łamigłówki publikowane przed wielu laty w prasie zagranicznej. Poniższa chyba ani tu, ani w innym rodzimym medium jeszcze nie gościła. Debiutowała w amerykańskim magazynie „Games” w sierpniu 1991 r. To dodawanie szkieletowe, w którym nie ujawniono żadnej cyfry.

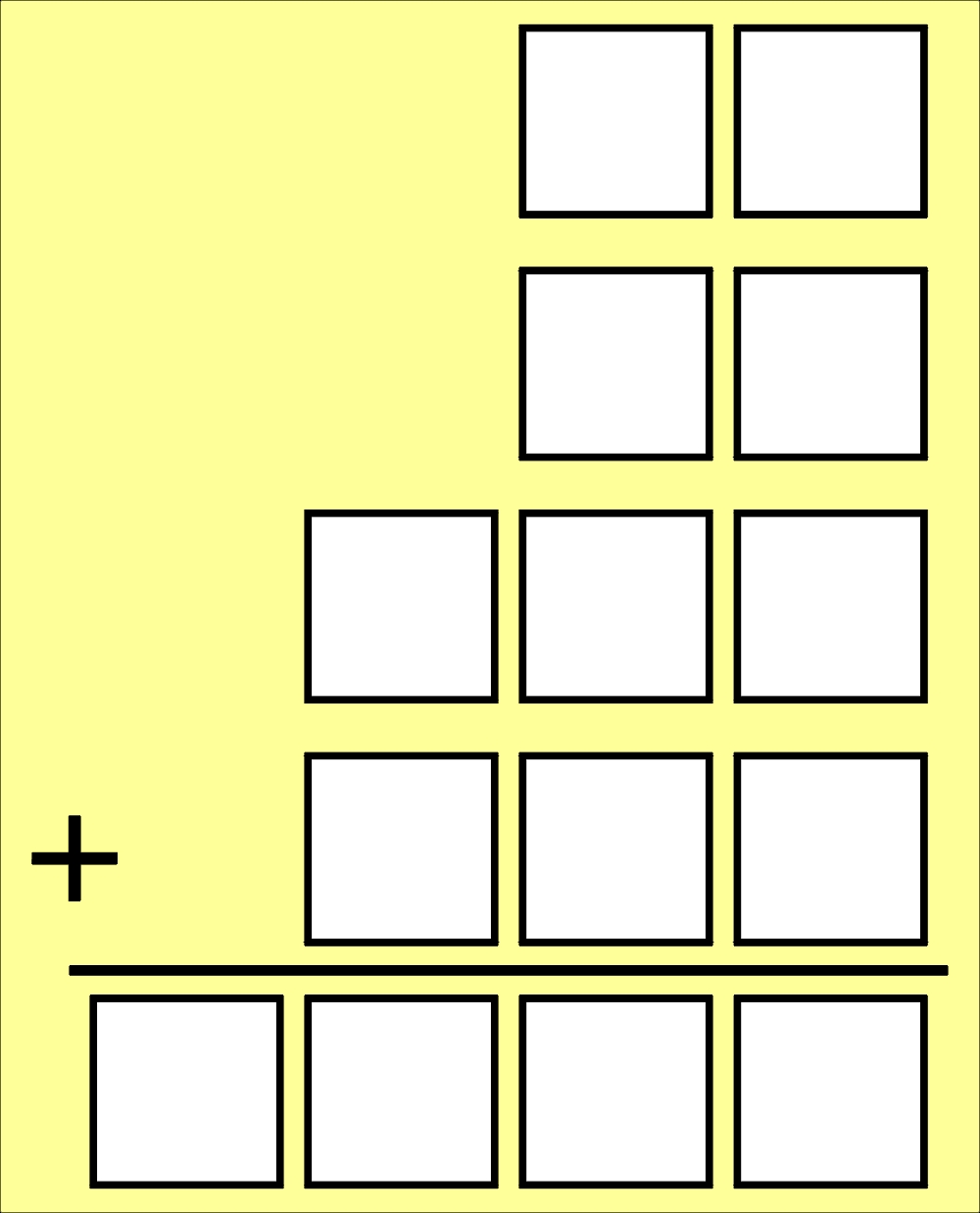
Pozostał tylko szkielecik w postaci zastępujących wszystkie cyfry kratek. Należy rozszyfrować działanie, korzystając z jednej krótkiej informacji: każda cyfra jest o 1 większa od znajdującej się bezpośrednio pod nią.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze

[lukasz_m]

74 + 63 + 752 + 641 = 1530
Fajne zadanie 🙂

[grgkh]

  74
  63
 752
+641
====
1530

[bubka111]

74
63
752
641
_____
1530

[Antyp1958]

Mamy:

1.wiersz: ba = 10b + a

2.wiersz: 10(b−1) + (a−1)

3.wiersz: 100c + 10(b−2) + (a−2)

4.wiersz: 100(c−1) + 10(b−3) + (a−3)

5.wynik: d(c−2)(b−4)(a−4)

Po zsumowaniu lewej strony i porównaniu z wynikiem wychodzi równanie:

30b+3a+100c+78=1000d, z ograniczeniami:
z ograniczeniami
, ∈{4…9}; c∈{2…9}, ∈{1…9}

Jedyna możliwość to d=1 wtedy 30b+3a+100c=922.

To równanie ma jedno rozwiązanie w cyfrach:

a=4,b=7,c=7,d=1.

74+63+752+641=1530,

—————————————–

ab
(c)(b−1)(a−1)
(c−1)(b−2)(a−2)
+(c−2)(b−3)(a−3)
———————–
d(c−3)(b−4)(a−4)
Tu znalazłem dwa rozwiązania:
a=4, b=7, c=4, d=1 → 74+463+352+241=1130
a=4, b=7, c=9, d=2 → 74+963+852+741=2630

5+4+3=12
4+3+2+1=10
4+53+42+31=130
74+63+52+41=230

[Qba]

74
63
752
641
——
1530

[Michał S]

Gdyby warunek „każda cyfra jest o 1 większa od znajdującej się pod nią” odnieść do wszystkich cyfr działania, to suma powinna być 1111, bo pod sumą nic nie ma czyli są tam zera. Niestety utworzone w ten sposób działanie 55+44+333+222=1111 jest błędne.

[jarek1962]

74+63+752+641=1530

[Spytko z Melsztyna]

 
__7,4
__6,3
_7,5,2
_6,4,1
--------
1,5,3,0
 

[kobert]

74+63+752+641=1530

[aps1968]

Sympatyczne zadanie, można właściwie rozwiązać w pamięci, patrząc tylko na schemat, albo i nie. Zaczyna się oczywiście od prawej i idzie w lewo, otrzymując 74+63+752+641=1530. Spróbowałem odwrotnie, czy da się tak, by cyfry rosły, a nie malały, z góry do dołu, ale wychodzi mi, że się nie da, przynajmniej w tym diagramie.

[Brzeszczot78]

__74
__63
_752
_641
———
1530

[uch_ty]

x x 7 4
x x 6 3
x 7 5 2
x 6 4 1
1 5 3 0