Kwadrat z kwadratów
Kwadrat ma w matematyce dwa znaczenia – algebraiczne i geometryczne, więc w tytule tego wpisu też mógłby mieć dwa.
Algebraiczne kojarzy się z trójkami pitagorejskimi, czyli kwadratem jako sumą dwóch kwadratów, np. 3^2+4^2=5^2 lub 18^2+24^2=30^2. Mogłyby być także czwórki pitagorejskie (np. 6^2+6^2+7^2=11^2), piątki (np. 5^2+6^2+12^2+18^2=23^2), szóstki, siódemki itd.
Znaczenie geometryczne to oczywiście kwadrat zbudowany z mniejszych kwadratów, z uwzględnieniem spektakularnego podproblemu składania kwadratu z mniejszych kwadratów różnej wielkości (wikipedia).
Poniższe zadanie jest inne, choć także geometryczne. Chodzi o podział figury złożonej z 8 kwadratów liniami prostymi na części, z których będzie można złożyć kwadrat. W przykładzie z lewej strony są dwie linie, które dzielą kwadrat na cztery części. Zadanie polega na podziale tej samej figury (z prawej) dwiema liniami na trzy części. Części te przy układaniu kwadratu wolno odwracać (odbicia lustrzane; jak w przykładzie).
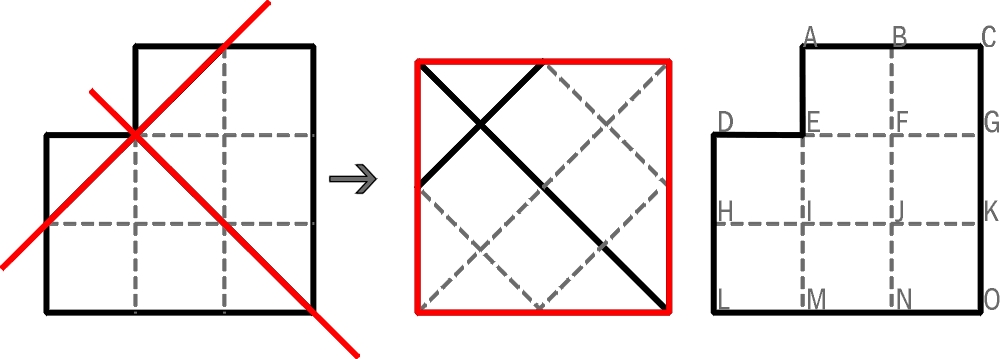
Rozwiązanie można podać tekstem, korzystając z oznaczeń literowych punktów, przez które będą przechodzić linie dzielące (rozwiązanie przykładu: B-E-H, E-J-O).
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
C-F-I; D-I-N; Zadanie jest bardzo łatwe. Wystarczy narysować te dwie figury i przesuwać jedną nad drugą. Po kilku ruchach rozwiązanie pojawia się samo.
AFK, FIL lub symetrycznie CFI, DIN
L-I-F
A-F-K
Jak wyrwać się z hipnotycznej sugestii?
Założyć rombowo-kwadratowe okulary. Dzielić na cztery, ale dwa kawałki wziąć jako jeden.
L-I-F, A-F-K
lub
D-I-N, I-F-C
Dla wynikowego kwadratu, o boku o jednostkę większego od podanego tutaj zadania, figurą do pocięcia powinna być powierzchnia składająca się z 2*3^2 małych kwadracików. Przymierzałem się do jej pocięcia, zaczynając od różnych jej kształtów, możliwie zwartych i starając się znaleźć najmniejszą ilość fragmentów, z których uda się ułożyć kwadrat.
Np. dla takiej figury podział na cztery części jest łatwy do odgadnięcia, a na trzy części, czy w ogóle jest możliwy? A dla innego kształtu figury wyjściowej?
x x x
x x x x
x x x x
x x x x
x x x
„x” oznacza tu pole jednostkowego kwadratu
DIN, CFI