Bliźniaki bis
„Raczej twardy orzech” w skali od 1 do 10 oznacza 7 – tak wyceniałem zadanie sprzed tygodnia. Natomiast dzisiejsze zasługuje moim zdaniem na 9.
Instrukcji obsługi nie przypominam. Odsyłam do poprzedniego wpisu, gdzie jest także określony sposób podania rozwiązania. Powtarzam tylko przykład.
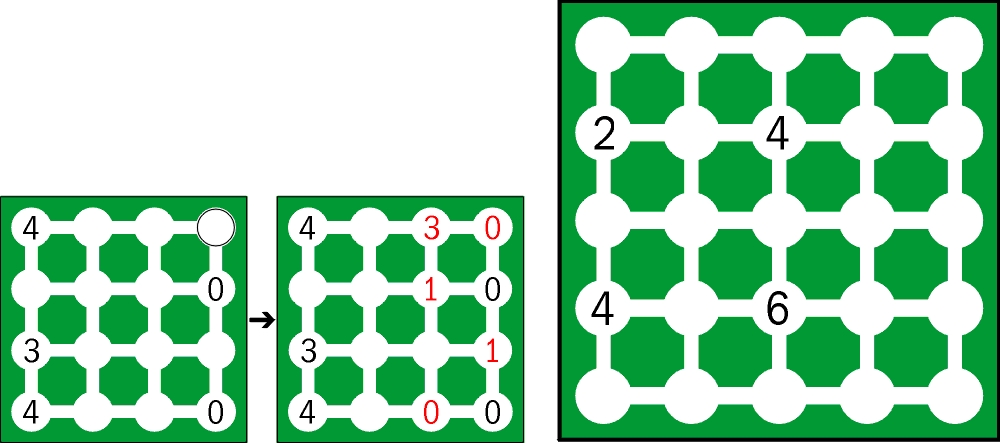
Po namyśle doszedłem jednak do wniosku, że warto przypomnieć jeszcze dodatkowy warunek, bo w nadsyłanych rozwiązaniach bliźniaków sprzed tygodnia bywał on pomijany. Otóż jeśli w diagramie z rozwiązaniem będą co najmniej dwie pary takich samych liczb X (jak dwie pary zer w przykładzie), to pary te musza być od siebie odizolowane. Inaczej pisząc: nie może być połączenia między liczbami X z różnych par, gdzie połączeniem jest biała droga wiodąca przez puste pola.
PS droga między bliźniakami (jednakowymi liczbami) powinna być jedyną możliwą, czyli nie może być dwóch dróg różniących się tylko jednym polem.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
3 P P P P
2 P 4 6 P
3 P P 1 4
4 2 6 P 1
P P P P 4
Bardzo sprytne i zoptymalizowane, wykorzystujące wszystkie pola jako części łączących ścieżek. Do rozwiązywania na kartce papieru niesłychanie niewygodne.
Liczby z minusem to te, które należało dopisać.
3PPPP/2P46P/3PP14/426P1/PPPP4
Wydaje mi się że wszystkie warunki są spełnione.
Chciałbym zaproponować dwa zadania mojego autorstwa ułożone według zasad Bliźniaków. Daleko im do elegancji zadań prezentowanych przez Gospodarza, a też nie mogę zagwarantować, że na pewno mają one tylko jedno rozwiązanie, choć sporo wysiłku włożyłem, by taki cel osiągnąć. Zakładając, że tak jest, poddaję je pod ocenę, z nadzieją, że osiągniecie rozwiązania będzie satysfakcjonujące.
Oba zadania są kwadratami – 7×7 oraz 8×8. Litery x zastępują pola puste.
Trwało to trochę dłużej niż przewidywałem, ale udało mi się dokończyć prosty programik, który nieco wspomaga uciążliwe wpisywanie na kartce w kratkę i wielokrotne gumkowanie nietrafionych wpisów podczas rozwiązywania tego zadania. Tu jest jego treść do pobrania:
https://share.evernote.com/note/c34a7a90-58e1-428a-797c-ea44d42cafd8
Razem z plikiem wspomagającym rozwiązywanie zamieściłem pliki tekstowe, które można wczytać do programu, unikając trudu ręcznego przepisywania treści. Dokładny opis programu jest w chmurze pod linkiem.
Zadania zamieszczam po uzyskaniu zgody Gospodarza. 🙂
W celu ustalenia trudności łamigłówki proponuję następujący wzór/metodę:
Trudność=10-ILO
(ILO=ilość poprawnych rozwiązań w pierwszym dniu).
W poprzedniej łamigłówce („Bliźniaki”) mieliśmy ILO=3 czyli trudność łamigłówki wynosi 7 (wartość chyba trochę zawyżona przez „szok poznawczy”).
Dla obecnej łamigłówki („Bliźniaki bis”) dane poznamy za kilka dni – po ich ujawnieniu.
Nasz Miły Gospodarz już wie…
🙂
@grgkh
Poniżej moje rozwiązanie (kropki to oczywiście puste pola).
Mam pozytywne wrażenia z rozwiązywania – nie było trudno 🙂
Wątpliwości są w miejscu, które oznaczyłem znakiem zapytania:
Pojawia się tu dodatkowe puste pole łączące obie piątki,siódemki,ósemki,dziewiątki.
To drobny niuans ale Gospodarz w swoim PS do ostatniej łamigłówki taką właśnie „usterkę” wskazuje.
Powyższe wątpliwości obowiązują oczywiście tylko jeśli moje rozwiązanie jest tym zaplanowanym (?).
Coraz bardziej lubię ten gatunek.
Za większy rozmiar zabiorę się w innym terminie.
Zadania, które umieściłem w poprzednim komentarzu, niestety, zawierają jedno odstępstwo od warunku, o którym przypomniał na końcu wpisu z tego tygodnia Gospodarz bloga. Otóż są w nich miejsca, w których, choć lokalizacja liczb pary jest zdeterminowana jednoznacznie, to szerokość prowadzącej drogi pomiędzy liczbami pary pozwala na wybieranie alternatywnych wariantów. Te alternatywne warianty najkrótszej trasy przylegają do siebie, jednak nie są jedynymi możliwymi. Mając świadomość tej ułomności, można je jednak rozwiązywać dochodząc do jednoznacznego wyniku. Na razie wstrzymam się ujawnieniem moich wariantów rozwiązań.
Zadania te układałem w poprzednim tygodniu a potem wysyłając tutaj nie zweryfikowałem pełnej zgodności z przypomnianymi warunkami. Winien był pośpiech. Przepraszam za zamieszanie, jakie z tego wynikło.
Mam jednak dwie nowe propozycje, tym razem w pełni zgodne z warunkami. Nie jestem pewien, czy „zanadto” nie okroiłem ilości ujawnionych liczb. Zadania zrobiły się przez to trudniejsze, ale – mam taką nadzieję – wciąż dające jedyne, jednoznaczne rozwiązanie.
W mniejszym diagramie jedno z pól jest niezagospodarowane, nie przebiega przez nie żadna ze ścieżek łączących pary liczb. W diagramie większym trzy spośród liczb mniejszych od największej ujawnionej w ogóle nie występują ale nie zdradzę, które to są.
============ Zadanie 3
Treść kwadratowych plansz (bez żadnych dodatków) można przekopiować do pustego pliku tekstowego, zapisać taki plik, a potem będzie on możliwy do odczytania przez program wspomagający, do którego podawałem link w poprzednim komentarzu.
3 P P P P
2 P 4 6 P
3 P P 1 4
4 2 6 P 1
P P P P 4
Wiersze od dołu do góry 1,2,3,4,5. Kolumny z lewa na prawo a,b,c,d,e. Słowa kluczowe: „najkrótsza droga przez puste pola”, „droga jedyna możliwa”, „dwie drogi różniące się jednym polem”,
Są dwie drogi między szóstkami: c3,b3,b4,b5,c5,d5 oraz c3,b3,b4,b5,c5,d5,e5,e4. Różnią się liczbą pól (dwoma polami), jedna krótsza, druga dłuższa, każda jest jedyna w swoim rodzaju pod względem długości. Dla nas jedyną możliwą jest krótsza, bo liczba pól jest równa liczbom, które łączy.
Między górnymi czwórkami są trzy drogi: 1)e4,e5,d5,c5, 2) e4,e5,d5,c5,b5,b4, 3) e4,e5,d5,c5,b5,b4,b3,c3. Dla nas jedyną możliwą jest jedyna 4-polowa (najkrótsza).
Spójrzmy na parę.
x P P P 6
x P x x x
x P P x x
x P 6 x x
x x x x x
P – puste pole, x – jakaś liczba
Są dwie drogi między szóstkami: d5,c5,b5,b4,b3,e3 oraz d5,c5,b5,b4,b3,b2. Różnią się jednym polem, ale liczba pól jest taka sama, żadna z nich nie jest jedyna. Nie możemy wybrać krótszej (jedynej).
@grgkh
Poniżej dwa rozwiązania zadania numer 3 (oba z usterkami ?).
6-dwie ścieżki
6-dwie ścieżki
Wysyłam oba bo mają istotne różnice więc może rozwiązań jest więcej niż jedno ?
Podam informacje dodatkowe, które mogą pomóc w odgadnięciu rozwiązania.
============== Zadanie3
W polu E2 jest liczba 6.
Suma wszystkich liczb występujących w diagramie wynosi 52.
============== Zadanie4
Oprócz liczb ujawnionych wcześniej, do których należy dodać uzupełniającą liczbę do pary, brakuje tylko dwóch liczb – 4 i 5, oczywiście też wpisanych podwójnie. Obie liczby 12 są w tej samej kolumnie – C. Para do 10 jest w wierszu ujawnionej 11, a para do 11 jest w wierszu ujawnionej 10.
@apartado
Zadanie 1 jest odgadnięte zgodnie z założeniami autora. Chyba już czas na prezentację rozwiązań pozostałych zadań.
@grgkh
Zadania o większych rozmiarach okazały się układami o nietrywialnej prostocie ;).
W zadaniu 3 ładna ta pułapka z dwójkami, które nie należą do jednej pary. Szkoda, że nie udało mi się znaleźć rozwiązania z dwiema parami, ale podejrzewam, że takie istnieje (moje dwa rozwiązania są „obiecujące” w tym zakresie).
@grgkh
Moja intuicyjna ocena dotycząca prawdopodobieństwa istnienia rozwiązania zadania 3 (z jedną parą dwójek) okazała się prorocza:
Przecież nadmieniałem, że coraz bardziej lubię ten gatunek 😉
„Bliźniaki na granicy chaosu”.
@apartado
Gratuluję. 🙂 Ładnie się przeplatają w tym wariancie ścieżki 5, 6 i 7. Przyznam się, że nie miałem czasu, a może trochę i zapału, by dłużej posprawdzać, czy akurat taki dobór ujawnionych liczb nie daje więcej niż jednego rozwiązania. Czym większa plansza i mniej ujawnionych liczb, tym prawdopodobieństwo większej ilości rozwiązań rośnie. Wtedy można rywalizować, kto znajdzie ich więcej. Ujawnione liczby wybierałem „na oko”, intuicyjnie.
A czy korzystałeś z programu pomocnika? Jeśli tak, to jak go oceniasz?
Do niektórych wcześniejszych zadań w Łamiblogu też sobie podobne programy robiłem. Eliminują uciążliwości wypisywania wariantów, a i staram się dodawać do nich możliwość tworzenia i rejestracji własnych zadań. Bez dodawania algorytmów wyszukujących wszystkie warianty rozwiązań, bo takie pozostawiam tylko do swojej dyspozycji. Na przyszłość mógłbym je umieszczać w chmurze evernote pod tym samym linkiem.
Takie ułatwianie rozwiązywania nie odbiera przyjemności odkrywania i zastosowania algorytmu, a może tych mniej cierpliwych powstrzymywać od porzucania zadania wydającego się zbyt żmudnym.
@grgkh
Program do tego byłby chyba bardzo skomplikowany – nie wchodźmy tu w niuanse.
Wczoraj znalazłem (także „ręcznie”) jeszcze jeden wariant w zadaniu 3.
(prosta modyfikacja par 44,77 z poprzedniego rozwiązania na pary 33,88).
@apartado
Nie jest skomplikowany, jest bardzo prosty. To można łatwo sprawdzić doświadczalnie. Jest tam też cały opis obsługi. Krótki. Dużą zaletą programu jest też obsługa zapisywania stanu planszy do pliku i odczytywania tego stanu, w dowolnym momencie i dla nieograniczonej ilości wariantów.