LiSty reaktywacja

Zadań diagramowych, w których występują strzałki, zebrałoby się ponad pół setki, ale większość z nich to takie, które po zaliczeniu debiutu w sieci lub w druku pojawiają się później bardzo rzadko lub wcale. Przed nastu laty w Łamiblogu gościły tzw. liczbostrzałki, czyli LiSty (w l. poj. LiSta) – elementy łamigłówek, będące połączeniem strzałek z liczbami. Poniższe zadanie także można zaliczyć do LiSt-owych. Jego reguły są proste (o rozwiązanie – jak się zapewne okaże – znacznie trudniej). Wygodnie będzie jednak zamiast typowego opisu przedstawić jako instrukcję jego… konstrukcję.

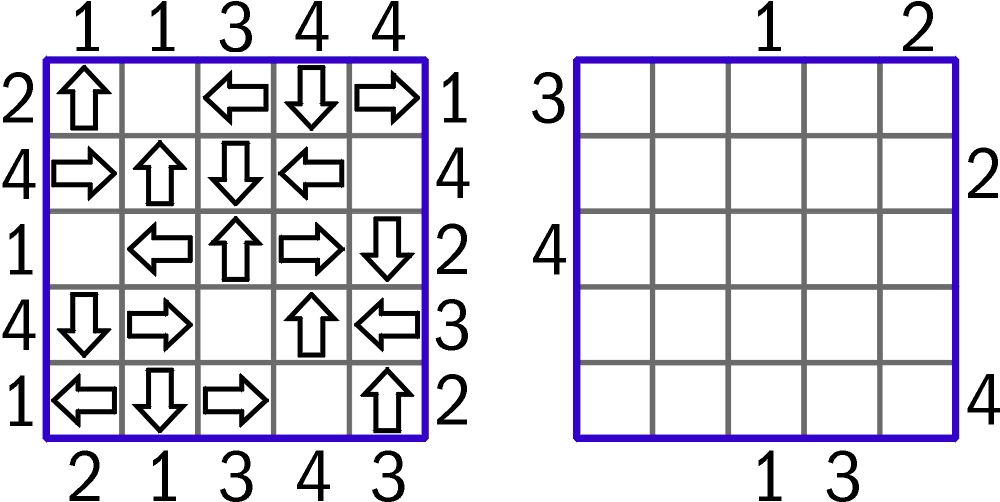
Na rysunku z lewej strony w diagramie są strzałki, a przy brzegach liczby. Całość stanowi jakby rozwiązanie z nadinformacją (komplet liczb to zdecydowanie za dużo). Co oznacza każda liczba? – to dodatkowa, ale łatwa zagadka. Ułożenie zadania – teoretycznie proste, praktycznie bardzo trudne – polega na usunięciu większości liczb. Pozostać powinna ich minimalna liczba, która pozwoli na jednoznaczne rozmieszczenie strzałek – takie, jak na diagramie. Łatwo zauważyć, że w każdym wierszu i w każdej kolumnie muszą się znaleźć cztery strzałki, a każda powinna wskazywać inny kierunek. Które liczby usunąć, aby powstało zadanie – nie wiem. Próbowałem, ale poddałem się, bo to benedyktyńskie zajęcie.
Zamiast tego diagram z prawej strony jest innym gotowym zadaniem. Uprzedzam, że mimo odgadnięcia, co oznaczają liczby, lekko nie będzie. Rozwiązanie można podać oznaczając kierunki strzałek w kolejnych rzędach. Na przykład w pierwszym rzędzie rozwiązania przykładu z nadinformacją: NXWSE-… (X – puste pole).

Komentarze

[apartado]

V.^
.^
^>.V<
.^V
><V^.

[apartado]

S.NWE
WSE.N
NE.SW
.NWES
EWSN.

[Spytko z Melsztyna]

Jeżeli brakująca reguła brzmi:
cyfra mówi, która strzałka (licząc od strony tej cyfry) wskazuje na tą cyfrę, to jest 40 rozwiązań:
1
('E', 'S', 'N', 'W', 'X')
('W', 'X', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['X', 'W', 'S', 'N', 'E']
('N', 'E', 'W', 'X', 'S')
---------------------------
2
('E', 'S', 'N', 'W', 'X')
('W', 'X', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['N', 'W', 'S', 'X', 'E']
('X', 'E', 'W', 'N', 'S')
---------------------------
3
('E', 'S', 'N', 'W', 'X')
('S', 'W', 'X', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['W', 'N', 'S', 'X', 'E']
('X', 'E', 'W', 'N', 'S')
---------------------------
4
('E', 'S', 'N', 'W', 'X')
('S', 'W', 'X', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['W', 'X', 'S', 'N', 'E']
('N', 'E', 'W', 'X', 'S')
---------------------------
5
('E', 'S', 'N', 'W', 'X')
('S', 'X', 'W', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['N', 'W', 'S', 'X', 'E']
('W', 'E', 'X', 'N', 'S')
---------------------------
6
('E', 'S', 'N', 'W', 'X')
('X', 'W', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['W', 'X', 'S', 'N', 'E']
('N', 'E', 'W', 'X', 'S')
---------------------------
7
('E', 'X', 'N', 'W', 'S')
('W', 'S', 'X', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['N', 'W', 'S', 'X', 'E']
('S', 'E', 'W', 'N', 'X')
---------------------------
8
('E', 'X', 'N', 'W', 'S')
('S', 'W', 'X', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['N', 'S', 'W', 'X', 'E']
('W', 'E', 'S', 'N', 'X')
---------------------------
9
('E', 'X', 'N', 'W', 'S')
('X', 'W', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['S', 'N', 'W', 'X', 'E']
('W', 'E', 'S', 'N', 'X')
---------------------------
10
('E', 'X', 'N', 'W', 'S')
('X', 'W', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['W', 'N', 'S', 'X', 'E']
('S', 'E', 'W', 'N', 'X')
---------------------------
11
('E', 'X', 'N', 'W', 'S')
('X', 'W', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['N', 'S', 'W', 'X', 'E']
('W', 'E', 'S', 'N', 'X')
---------------------------
12
('S', 'E', 'N', 'W', 'X')
('W', 'S', 'X', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['X', 'W', 'S', 'N', 'E']
('E', 'N', 'W', 'X', 'S')
---------------------------
13
('S', 'E', 'N', 'W', 'X')
('W', 'S', 'X', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['N', 'W', 'S', 'X', 'E']
('E', 'X', 'W', 'N', 'S')
---------------------------
14
('S', 'E', 'N', 'W', 'X')
('W', 'X', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['X', 'W', 'S', 'N', 'E']
('E', 'N', 'W', 'X', 'S')
---------------------------
15
('S', 'E', 'N', 'W', 'X')
('X', 'W', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['W', 'X', 'S', 'N', 'E']
('E', 'N', 'W', 'X', 'S')
---------------------------
16
('S', 'E', 'N', 'W', 'X')
('X', 'W', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['W', 'N', 'S', 'X', 'E']
('E', 'X', 'W', 'N', 'S')
---------------------------
17
('S', 'E', 'N', 'W', 'X')
('X', 'S', 'W', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['W', 'N', 'S', 'X', 'E']
('E', 'W', 'X', 'N', 'S')
---------------------------
18
('S', 'X', 'N', 'W', 'E')
('W', 'S', 'E', 'X', 'N')
('N', 'E', 'X', 'S', 'W')
['X', 'N', 'W', 'E', 'S']
('E', 'W', 'S', 'N', 'X')
---------------------------
19
('S', 'X', 'N', 'W', 'E')
('W', 'S', 'E', 'X', 'N')
('E', 'N', 'X', 'S', 'W')
['N', 'W', 'S', 'E', 'X']
('X', 'E', 'W', 'N', 'S')
---------------------------
20
('S', 'X', 'N', 'W', 'E')
('W', 'S', 'X', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['E', 'W', 'S', 'N', 'X']
('N', 'E', 'W', 'X', 'S')
---------------------------
21
('S', 'X', 'N', 'W', 'E')
('W', 'S', 'X', 'E', 'N')
('X', 'N', 'E', 'S', 'W')
['N', 'E', 'W', 'X', 'S']
('E', 'W', 'S', 'N', 'X')
---------------------------
22
('S', 'X', 'N', 'W', 'E')
('X', 'W', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['W', 'E', 'S', 'N', 'X']
('E', 'N', 'W', 'X', 'S')
---------------------------
23
('S', 'X', 'N', 'W', 'E')
('X', 'W', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['E', 'N', 'W', 'X', 'S']
('W', 'E', 'S', 'N', 'X')
---------------------------
24
('S', 'X', 'N', 'W', 'E')
('X', 'W', 'E', 'S', 'N')
('E', 'S', 'X', 'N', 'W')
['W', 'N', 'S', 'E', 'X']
('N', 'E', 'W', 'X', 'S')
---------------------------
25
('S', 'X', 'N', 'W', 'E')
('X', 'S', 'W', 'E', 'N')
('N', 'E', 'X', 'S', 'W')
['W', 'N', 'E', 'X', 'S']
('E', 'W', 'S', 'N', 'X')
---------------------------
26
('S', 'X', 'N', 'W', 'E')
('X', 'S', 'W', 'E', 'N')
('E', 'N', 'X', 'S', 'W')
['N', 'W', 'E', 'X', 'S']
('W', 'E', 'S', 'N', 'X')
---------------------------
27
('X', 'E', 'N', 'W', 'S')
('W', 'S', 'X', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['S', 'N', 'W', 'X', 'E']
('E', 'W', 'S', 'N', 'X')
---------------------------
28
('X', 'E', 'N', 'W', 'S')
('W', 'X', 'E', 'S', 'N')
('N', 'S', 'X', 'E', 'W')
['S', 'N', 'W', 'X', 'E']
('E', 'W', 'S', 'N', 'X')
---------------------------
29
('X', 'E', 'N', 'W', 'S')
('W', 'X', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['N', 'S', 'W', 'X', 'E']
('E', 'W', 'S', 'N', 'X')
---------------------------
30
('X', 'E', 'N', 'W', 'S')
('W', 'X', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['N', 'W', 'S', 'X', 'E']
('E', 'S', 'W', 'N', 'X')
---------------------------
31
('X', 'E', 'N', 'W', 'S')
('S', 'W', 'X', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['W', 'N', 'S', 'X', 'E']
('E', 'S', 'W', 'N', 'X')
---------------------------
32
('X', 'S', 'N', 'W', 'E')
('W', 'X', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['E', 'W', 'S', 'N', 'X']
('N', 'E', 'W', 'X', 'S')
---------------------------
33
('X', 'S', 'N', 'W', 'E')
('W', 'X', 'E', 'S', 'N')
('S', 'N', 'X', 'E', 'W')
['N', 'E', 'W', 'X', 'S']
('E', 'W', 'S', 'N', 'X')
---------------------------
34
('X', 'S', 'N', 'W', 'E')
('W', 'X', 'E', 'S', 'N')
('S', 'E', 'X', 'N', 'W')
['N', 'W', 'S', 'E', 'X']
('E', 'N', 'W', 'X', 'S')
---------------------------
35
('X', 'S', 'N', 'W', 'E')
('S', 'W', 'E', 'X', 'N')
('N', 'E', 'X', 'S', 'W')
['W', 'N', 'S', 'E', 'X']
('E', 'X', 'W', 'N', 'S')
---------------------------
36
('X', 'S', 'N', 'W', 'E')
('S', 'W', 'E', 'X', 'N')
('E', 'N', 'X', 'S', 'W')
['N', 'X', 'W', 'E', 'S']
('W', 'E', 'S', 'N', 'X')
---------------------------
37
('X', 'S', 'N', 'W', 'E')
('S', 'W', 'X', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['W', 'E', 'S', 'N', 'X']
('E', 'N', 'W', 'X', 'S')
---------------------------
38
('X', 'S', 'N', 'W', 'E')
('S', 'W', 'X', 'E', 'N')
('N', 'X', 'E', 'S', 'W')
['E', 'N', 'W', 'X', 'S']
('W', 'E', 'S', 'N', 'X')
---------------------------
39
('X', 'S', 'N', 'W', 'E')
('S', 'X', 'W', 'E', 'N')
('N', 'E', 'X', 'S', 'W')
['W', 'N', 'E', 'X', 'S']
('E', 'W', 'S', 'N', 'X')
---------------------------
40
('X', 'S', 'N', 'W', 'E')
('S', 'X', 'W', 'E', 'N')
('E', 'N', 'X', 'S', 'W')
['N', 'W', 'E', 'X', 'S']
('W', 'E', 'S', 'N', 'X')
---------------------------

[Spytko z Melsztyna]

 
Ooops !!! Pominąłem w programie jeden logiczny krok. Rozwiązanie jest tylko jedno:
['S', 'X', 'N', 'W', 'E']
['W', 'S', 'E', 'X', 'N']
['N', 'E', 'X', 'S', 'W']
['X', 'N', 'W', 'E', 'S']
['E', 'W', 'S', 'N', 'X']
Przeprzszam za zamieszanie  :) 

[Antyp1958]

0 0 3 4 4 G
0 0 0 0 3 D
2 0 0 0 0 L
0 4 0 0 0 P

Minimalna ilość liczb do lewego diagramu. Nie sprawdzałem czy są inne układy. G-góra itd.

[ersonasolidna]

Panie Marku,
Trochę nie na temat, ale to chyba najlepsze miejsce. Nasz Bardzo Lokalny Komitet Rozwiązywaczy Zadań ze Świata Nauki nie rozumie ostatniego zdania-przykładu w zadaniu 1 z październikowego numeru:
„Na przykład: gdyby liczbami tymi były 2 i 6, to odpowiedzią byłby wzór dla x>0.”
Dlaczego x>0 miałoby być wzorem wskazującym na 2 i 6?
Znalezienie liczb, które nie są OSC żadnej szczęściary nie nastręcza problemów, ale ubranie tego w ogólny wzór na podstawie powyższego przykładu – już tak:)

Szanowny BLKRZzŚN,
z nieznanych mi powodów z druku wypadł sam wzór, który znajdował się między „wzór” a „dla” i był zapisany przy pomocy narzędzi równań (może dlatego został „maszynowo” wycięty).
mp