P + S(P)
W poprzednim wpisie opisana była następująca zabawa liczbowa:
Zaczynamy od dowolnej liczby złożonej Z i tworzymy sumę S(1)= Z+sopfr(Z), gdzie sopfr(Z) jest sumą wszystkich (nie tylko różnych) czynników pierwszych Z; tak samo postępujemy z S(1) i z każdą następną sumą dotąd, aż suma ta okaże się liczbą pierwszą, która finalizuje zabawę, czyli kończy ciąg liczb złożonych. Koronne pytanie brzmiało: jak daleko uda się Z-zajechać przy ograniczeniu zakresu Z do 1000. Okazało się, że ciąg liczb złożonych może liczyć maksymalnie 20 wyrazów, jeśli Z=183: 183, 247, 279, 316, 309, 428, 539, 564, 618, 726, 753, 1007, 1079, 1175, 1232, 1258, 1314, 1395, 1437, 1919. Następny wyraz (1919+101+19=2039) jest już liczbą pierwszą. A totalnie z problemem rozprawił się jarek1962, poszerzając zakres Z najpierw do miliona (w ciągu są wówczas maksymalnie 123 liczby złożone, gdy na początku jest 153633), a potem sięgając miliardów (szczegóły w komentarzach).
Tym razem chodzi o zabawę częściowo odwrotną, bo od liczby pierwszej P się zaczynającą. Ta pierwsza P i każda następna poddawana jest prostej „obróbce” – tworzony jest ciąg, w którym każdy kolejny wyraz jest sumą poprzedniego wyrazu i sumy jego cyfr, czyli P(n)=P(n-1)+S[P(n-1)]. Tak się dzieje dotąd, aż pojawi się kończąca ciąg liczba złożona.
Dla jednocyfrowych P ciąg się w ogóle nie zaczyna. Zacząłem więc od 11 i dość długo wyciągałem ciągi, dziwiąc się, że żaden nie chce przekroczyć trzech wyrazów. Dopiero startujący od 277 sięgnął kwartetu: 277, 293, 307, 317. Potem bardzo długo nie było 5-wyrazowego. Przez chwilę zastanawiałem się nawet nad możliwością znalezienia dowodu, że cztery wyrazy to maksimum. Dopiero 1559 stanowiło przełom, choć zaczyna drugi ciąg także 4-wyrazowy: 1559, 1579, 1601, 1609. Mając dwie odległe liczby startowe ciągów-kwartetów skorzystałem z OEIS i tu trafiłem na serię ciągów autorstwa znanego mi skądinąd holenderskiego liczbomana Patricka de Geesta – od A048523 do A048527. Każdy ciąg obejmuje liczby pierwsze, które zaczynają ciągi n-wyrazowe, dla 1<n<7. Dla n=6 na starcie jest ponad półmilionowa pierwszość: 516493, 516521, 516541, 516563, 516589, 516623; dopiero siódmy wyraz (516646) jest liczbą złożoną.
Czy ktoś z programistów pokusi się o kontynuację poszukiwań Patricka, czyli znalezienie liczby pierwszej rozpoczynającej 7-wyrazowy ciąg liczb pierwszych tworzonych w opisany sposób?
Natomiast „piechurom” proponuję pełen pierwszości słupkowy zapis mnożenia szkieletowego, w którym wszystkie cyfry zastąpiono kratkami:
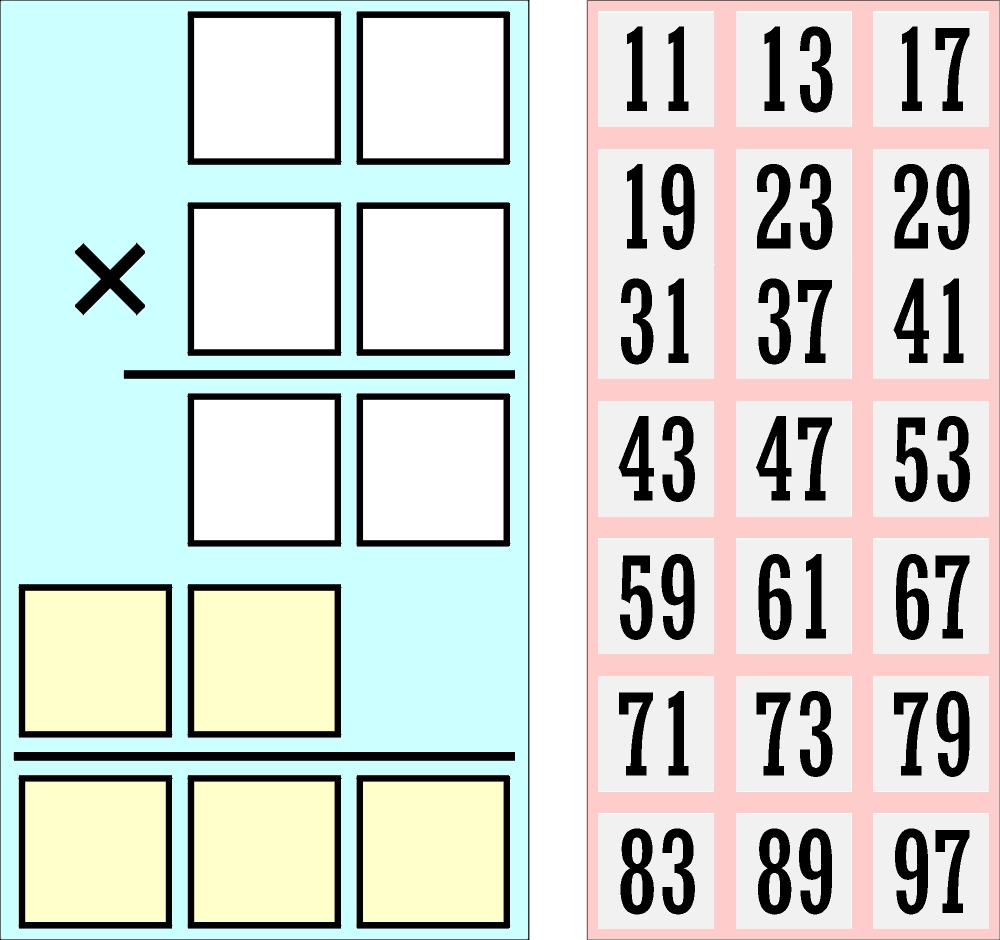
Mimo, że żadna cyfra nie jest ujawniona, zadanie nie wydaje mi się zbyt trudne, zwłaszcza, że ma więcej niż jedno rozwiązanie; wiadomo tylko, że wszystkie pięć liczb, występujących w zapisie, to liczby pierwsze – ale dwie dolne (żółtawe kratki) są… zapisane wspak. Dla wygody załączam komplet 2-cyfrowych liczb pierwszych; łatwo zauważyć, że trzy z nich ( a nie cztery) powinny trafić do mnożenia.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
1854778853,
8 wyrazów
1854778853, 1854778909, 1854778967, 1854779029,,1854779081, 1854779131, 1854779177, 1854779233. Poniżej miliarda jest kilkanaście o długości 7. Do dwóch miliardów :
start,długość ciąg
1061258971,7,1061258971 1061259011 1061259037 1061259071 1061259103 1061259131 1061259160
1102033783,7,1102033783 1102033811 1102033831 1102033853 1102033879 1102033913 1102033936
1198697957,7,1198697957 1198698019 1198698071 1198698121 1198698167 1198698223 1198698272
1253065897,7,1253065897 1253065943 1253065981 1253066021 1253066047 1253066081 1253066113
1253105083,7,1253105083 1253105111 1253105131 1253105153 1253105179 1253105213 1253105236
1287891901,7,1287891901 1287891947 1287892003 1287892043 1287892087 1287892139 1287892189
1321377877,7,1321377877 1321377923 1321377961 1321378001 1321378027 1321378061 1321378093
1377545891,7,1377545891 1377545941 1377545987 1377546043 1377546083 1377546127 1377546170
1403171173,7,1403171173 1403171201 1403171221 1403171243 1403171269 1403171303 1403171326
1428494891,7,1428494891 1428494941 1428494987 1428495043 1428495083 1428495127 1428495170
1430240293,7,1430240293 1430240321 1430240341 1430240363 1430240389 1430240423 1430240446
1446149933,7,1446149933 1446149977 1446150029 1446150061 1446150089 1446150127 1446150158
1451406991,7,1451406991 1451407031 1451407057 1451407091 1451407123 1451407151 1451407180
1467855947,7,1467855947 1467856003 1467856043 1467856087 1467856139 1467856189 1467856244
1507050073,7,1507050073 1507050101 1507050121 1507050143 1507050169 1507050203 1507050226
1565499799,7,1565499799 1565499863 1565499919 1565499977 1565500039 1565500073 1565500105
1567917947,7,1567917947 1567918003 1567918043 1567918087 1567918139 1567918189 1567918244
1586856863,7,1586856863 1586856919 1586856977 1586857039 1586857091 1586857141 1586857187
1606242991,7,1606242991 1606243031 1606243057 1606243091 1606243123 1606243151 1606243180
1663757861,7,1663757861 1663757911 1663757957 1663758013 1663758053 1663758097 1663758149
1698172871,7,1698172871 1698172921 1698172967 1698173023 1698173063 1698173107 1698173150
1714549913,7,1714549913 1714549957 1714550009 1714550041 1714550069 1714550107 1714550138
1776186851,8,1776186851 1776186901 1776186947 1776187003 1776187043 1776187087 1776187139 1776187189
1776186901,7,1776186901 1776186947 1776187003 1776187043 1776187087 1776187139 1776187189
1851502897,7,1851502897 1851502943 1851502981 1851503021 1851503047 1851503081 1851503113
1854778909,7,1854778909 1854778967 1854779029 1854779081 1854779131 1854779177 1854779233
1855202887,7,1855202887 1855202933 1855202971 1855203011 1855203037 1855203071 1855203103
1885557977,7,1885557977 1885558039 1885558091 1885558141 1885558187 1885558243 1885558292
1896495947,7,1896495947 1896496009 1896496061 1896496111 1896496157 1896496213 1896496262
1900327943,7,1900327943 1900327981 1900328021 1900328047 1900328081 1900328113 1900328141
1994656967,7,1994656967 1994657029 1994657081 1994657131 1994657177 1994657233 1994657282
19
× 41
——
19 ← 19×1 = 19 (pierwsza)
67 (od tyłu) ← naprawdę 76 = 19×4
——
977 (od tyłu) ← naprawdę 779 = 19×41
23
× 41
——
23 ← 23×1 = 23 (pierwsza)
29 (od tyłu) ← naprawdę 92 = 23×4
——
349 (od tyłu) ← naprawdę 943 = 23×41
Przykład siódemki, niekoniecznie najmniejszej:
2115112225943
2115112225981
2115112226021
2115112226047
2115112226081
2115112226113
2115112226141
A oto mniejsza siódemka (też nie wiem czy najmniejsza):
5083007887
5083007933
5083007971
5083008011
5083008037
5083008071
5083008103
Wklepanie 5083007887 w OEIS prowadzi do A320878 oraz https://www.primepuzzles.net/puzzles/puzz_163.htm
Meldunek odnośnie wpisu z 20 września 2025 – Pierwsza lepsza:
a1=8847
a2=8177
długość ciągu=7316
długość ostatniego wyrazu=1533
19*41=19+10*76=779
23*41=23+10*92=943
Okazuje się, że jako pierwszy zameldował się ciąg liczb pierwszych od razu o długości aż 8:
[286330897, 286330943, 286330981, 286331021, 286331047, 286331081, 286331113, 286331141, (286331170)]
Szukamy dalej…
Pierwsza siedmio jest też pierwsza ośmio:
286330897
286330943
286330981
286331021
286331047
286331081
286331113
286331141
Wieczorny meldunek.
Pierwsza liczba w każdym wierszu jest długością listy na której ostatnim wyrazem jest liczba niepierwsza.
9 [286330897, 286330943, 286330981, 286331021, 286331047, 286331081, 286331113, 286331141, 286331170] 2025-10-05 18:56:46.280065
8 [286330943, 286330981, 286331021, 286331047, 286331081, 286331113, 286331141, 286331170] 2025-10-05 18:56:46.280884
8 [388098901, 388098947, 388099003, 388099043, 388099087, 388099139, 388099189, 388099244] 2025-10-05 19:02:03.596320
8 [955201943, 955201981, 955202021, 955202047, 955202081, 955202113, 955202141, 955202170] 2025-10-05 19:27:22.159503
8 [1776186851, 1776186901, 1776186947, 1776187003, 1776187043, 1776187087, 1776187139, 1776187189] 2025-10-05 20:18:13.332544
8 [1854778853, 1854778909, 1854778967, 1854779029, 1854779081, 1854779131, 1854779177, 1854779233] 2025-10-05 20:23:20.387703
8 [2559495863, 2559495919, 2559495977, 2559496039, 2559496091, 2559496141, 2559496187, 2559496243] 2025-10-05 21:27:19.231397
8 [2647782901, 2647782947, 2647783003, 2647783043, 2647783087, 2647783139, 2647783189, 2647783244] 2025-10-05 21:35:26.657715
8 [3517793911, 3517793957, 3517794013, 3517794053, 3517794097, 3517794149, 3517794199, 3517794254] 2025-10-05 22:54:20.361965
8 [3628857863, 3628857919, 3628857977, 3628858039, 3628858091, 3628858141, 3628858187, 3628858243] 2025-10-05 23:03:12.596371
8 [3866728909, 3866728967, 3866729029, 3866729081, 3866729131, 3866729177, 3866729233, 3866729282] 2025-10-05 23:42:55.769323
8 [3974453911, 3974453957, 3974454013, 3974454053, 3974454097, 3974454149, 3974454199, 3974454254] 2025-10-05 23:56:56.545422
Starting prime: 286330897 (The maximum limit is set at 100,000,000)
Sequence length: 8
Sequence:
[286330897, 286330943, 286330981, 286331021, 286331047, 286331081, 286331113, 286331141]
Calculation time: 585.259 seconds
Fixing max limit:
Starting prime: 286330897 (The maximum limit is set at 1,000,000,000)
Sequence length: 8
Sequence:
[286330897, 286330943, 286330981, 286331021, 286331047, 286331081, 286331113, 286331141]
Calculation time: 585.259 seconds
Analiza czasu wykonywania obliczeń:
machine: language:
Intel® Core™ Ultra 7 258V (Lunar Lake) Python3.12
+———–+———–+
| seq_len | time [s] |
+———–+———–+
| 5 | ~0 |
| 6 | 0.2 |
| 7 | 159.4 |
| 8 | 585.3 |
| 9 | 12116.6(*)|
+———-+———–+
(*) Pomimo ponad 3,3 godziny obliczeń, nie udało się odnaleźć sekwencji dziewięciu liczb pierwszych. Ostatnią liczbą pierwszą przetestowaną przez mój program była 9999999967
1056493
1056521
1056541
1056563
1056589
1056623
Poranny meldunek przynosi drugą 9 czyli mamy drugi ciąg liczb pierwszych o długości 8:
8 [4167637819, 4167637871, 4167637921, 4167637967, 4167638023, 4167638063, 4167638107, 4167638150] 2025-10-06 02:44:52.088967
8 [4269837799, 4269837863, 4269837919, 4269837977, 4269838039, 4269838091, 4269838141, 4269838187] 2025-10-06 02:52:05.278672
8 [5083007887, 5083007933, 5083007971, 5083008011, 5083008037, 5083008071, 5083008103, 5083008131] 2025-10-06 03:50:00.050866
8 [5362197829, 5362197881, 5362197931, 5362197977, 5362198033, 5362198073, 5362198117, 5362198160] 2025-10-06 04:09:56.936981
8 [5642510933, 5642510971, 5642511011, 5642511037, 5642511071, 5642511103, 5642511131, 5642511160] 2025-10-06 04:29:46.526956
8 [6034811933, 6034811971, 6034812011, 6034812037, 6034812071, 6034812103, 6034812131, 6034812160] 2025-10-06 04:57:38.004922
8 [8180784851, 8180784901, 8180784947, 8180785003, 8180785043, 8180785087, 8180785139, 8180785189] 2025-10-06 07:30:07.356719
8 [8214319903, 8214319943, 8214319987, 8214320039, 8214320071, 8214320099, 8214320137, 8214320168] 2025-10-06 07:32:29.621068
8 [9045257839, 9045257891, 9045257941, 9045257987, 9045258043, 9045258083, 9045258127, 9045258170] 2025-10-06 08:31:36.353394
8 [9406983799, 9406983863, 9406983919, 9406983977, 9406984039, 9406984091, 9406984141, 9406984187] 2025-10-06 08:57:26.549942
8 [9512747861, 9512747911, 9512747957, 9512748013, 9512748053, 9512748097, 9512748149, 9512748199] 2025-10-06 09:05:00.369936
9 [10858338851, 10858338901, 10858338947, 10858339003, 10858339043, 10858339087, 10858339139, 10858339189, 10858339244] 2025-10-06 10:43:46.273811
8 [10858338901, 10858338947, 10858339003, 10858339043, 10858339087, 10858339139, 10858339189, 10858339244] 2025-10-06 10:43:46.273811
Przykład dziesiątki, zapewne nie jest najmniejszy:
1367618706414097919365699429
1367618706414097919365699571
1367618706414097919365699711
1367618706414097919365699847
1367618706414097919365699993
1367618706414097919365700141
1367618706414097919365700257
1367618706414097919365700381
1367618706414097919365700503
1367618706414097919365700621
19*41
23*41
Dwie kolejne „dziewiątki” (krótszych nie odnotowujemy), czyli 8-elementowe ciągi liczb pierwszych:
9 [12869802851, 12869802901, 12869802947, 12869803003, 12869803043, 12869803087, 12869803139, 12869803189, 12869803244] 2025-10-07 06:06:25.085747
9 [15845166851, 15845166901, 15845166947, 15845167003, 15845167043, 15845167087, 15845167139, 15845167189, 15845167244] 2025-10-07 09:38:02.608100
Problem piechurów ma dwa rozwiązania:
1) 19 * 41
2) 23 * 41
Mnożenie szkieletowe: jeśli liczby od góry oznaczymy A, B, C, D, E, to C może być liczbą pierwszą tylko jako wynik mnożenia Ax1, de facto mamy więc A, B, A, D, E, i B należy wybrać z grona: 11, 31, 41, 61, 71. Jeśli B = 11, to E jest podzielne przez 11, i tak samo gdy ustawimy cyfry w odwrotnej kolejności, np. 31×11 = 341 i 143 też się dzieli przez 11, dokładnie jest to 13×11. Jeśli B = 31 lub 61, to liczba D jest podzielna przez 3 i taką pozostaje po zmianie kolejności cyfr. Dla B = 71 nie ma zbyt wielu możliwości, bo iloczyn robi się szybko 4-cyfrowy, zostaje A = 11 lub 13, 11 już wykluczyliśmy, a 13 się nie zgadza, iloczyn jest 923, a liczba 329 nie jest pierwsza. Zostaje 41 i dla A = 19 wszystko się zgadza, D = 76, E = 779, liczby 67 i 977 są pierwsze. Podobnie A = 23: D = 92, E = 943, liczby 29 i 349 są pierwsze.
jarek1962,
Jestem super ciekawy, jak długo Twój algorytm szukał tej dziesiątki i na jakiej maszynie to liczyłeś.