Rok wesoły
Wszystkie liczby naturalne dodatnie dzielą się na wesołe i smutne. Rolę klasyfikatora pełni następujący algorytm:
1) oblicz sumę S kwadratów cyfr liczby X;
2) jeśli S>1 oblicz sumę kwadratów cyfr sumy S;
3) powtarzaj krok 2 z każdą kolejną sumą dotąd, aż:
a) pojawi się S=X lub powtórzy się S>1 – wtedy X jest liczbą smutną,
b) pojawi się S=1 – wtedy X jest liczbą wesołą.
Nowy rok za pasem. Sprawdźmy, czy przypisana mu liczba zwiastuje smutek czy wesołość:
2026 –> 4+0+4+36=44
44 –> 16+16=32
32 –> 9+4=13
13 –> 1+9=10
10 –> 1+0=1
Zatem można się uśmiechnąć, a potem sprawdzić, że rok miniony (2025) i ten, który zacznie się za rok (2027) to smutasy.
Pozostając przy specyficznych własnościach 2026 warto wspomnieć, że liczba ta zajmuje 582. miejsce w ciągu liczb półpierwszych, czyli jest iloczynem dwóch liczb pierwszych (2×1013), a znajduje się dokładnie w połowie drogi między poprzednią półpierwszą (2021=43×47), a następną (2031=3×677). Znacznie lepsze pozycje zajmuje w dwóch pokrewnych sekwencjach: 38. w ciągu liczb półpierwszych o 1 mniejszych od liczby pierwszej i 19. wśród takich liczb o 1 większych od kwadratu. Reasumując: należy do rodzynków wciśniętych między liczbę pierwszą a kwadrat – takich rarytasów jest do miliona tylko (nomen omen, choć bez zera) – 226.
Inne cechy wyróżniające 2026 należą do mocno wyszukanych, więc wymagałyby dodatkowych wyjaśnień albo odsyłania do specjalistycznych publikacji lub chociaż do Wikipedii. Na przykład:
– 2026 to jedenasta liczba Eulera II rzędu, będąca wynikiem działania 2^n–2*n, dla n=11;
– 2026 równa się liczbie kompozycji liczby 12 na co najwyżej 8 składników. Kompozycja jest partycją liczby, w której kolejność składników jest istotna. Wyjaśnieniem obu pojęć może być przykład: partycji liczby 4 jest pięć: 4, 3+1, 2+2, 2+1+1, 1+1+1+1; natomiast kompozycji liczby 4 mamy osiem: 4, 3+1, 1+3, 2+2, 2+1+1, 1+2+1, 1+1+2, 1+1+1+1.
Pora na zadanie, które jest tradycyjnym noworocznym „3 po 3”, choć nieco zmodyfikowanym.
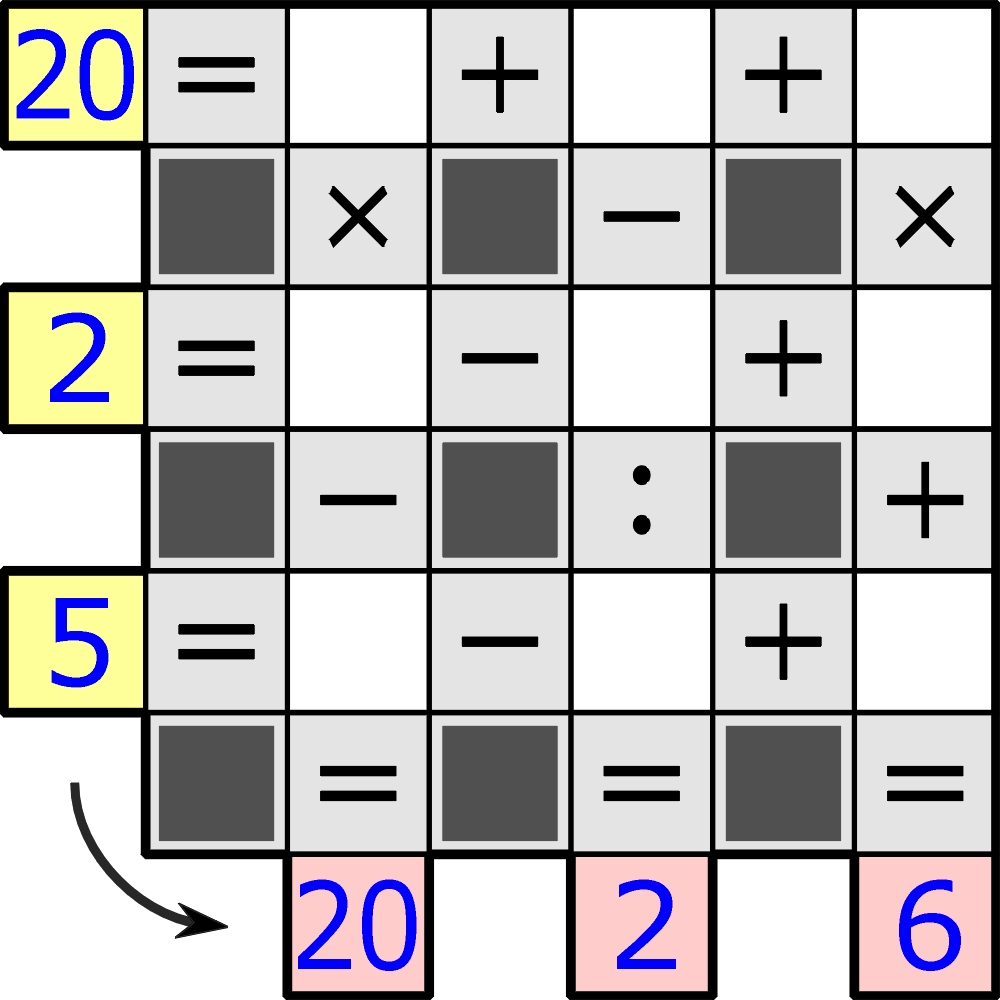
Chodzi o rozmieszczenie w białych kratkach dziewięciu różnych cyfr tak, aby wskazane działania w trzech wierszach i trzech kolumnach były poprawne. Działania należy wykonywać po kolei, czyli bez przestrzegania pierwszeństwa mnożenia i dzielenia (uwaga ta dotyczy właściwie tylko drugiej kolumny). Wspomniana modyfikacja wiąże się z zakresem liczb. Tradycyjnie do kratek wpisywane są różne cyfry od 1 do 9. Tym razem należy uwzględnić także zero, czyli w działaniach zabraknie jednej z pozostałych cyfr.
A na koniec takie poczwórne dziwadło: (20/2-6)*(20*26)-(20+26)-(20-2*6)=2026. Kto da krócej?
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
3, 9, 8
7, 5, 0
1, 2, 6
Spokojnego i sympatycznego 2026
W drugim zadaniu można wykorzystać tylko cyfry 0,2,6 ? czy trzeba grupami 20,26; 2,0,26; 20,2,6 itd . Czy krócej oznacza jak najmniej znaków (cyfr, nawiasów, znaków działań)?
Nie precyzowałem reguł, czyli wg uznania, ale jakoś ambitnie. Może tak: jak najkrócej z wykorzystaniem tylko 0, 2 i 6 i bez liczb dłuższych niż 2-cyfrowe, bo przy 3-cyfrowych można np. tak: 600*6/2+226.
mp
20=3+9+8
2=7-5+0
5=1-2+6
2×(26+6)^2-22
3, 9, 8,
7, 5, 0,
1, 2, 6
Szczęśliwego 2026 roku dla Gospodarza i wszystkich Łamiblogowiczów 🙂
Zadanie tradycyjne:
3 9 8
7 5 0
1 2 6
Zadanie drugie – może później:)
No to dokładnie wg reguł z przykładu lecz o 1/4 krócej (z użyciem silni):
(2^0+2)*6!-(20+2)*6+(2+0+2-6) =2026
3 + 9 + 8 = 20 * - * 7 - 5 + 0 = 2 - : + 1 - 2 + 6 = 5 === === === 20 2 626*2^6+6^2*20/2+2=2026
20⋅2^6+6!+26=2026
Myślę, że oba są „jakoś ambitnie”.
Z okazji Nowego Roku składam serdeczne życzenia zdrowia, spokoju i nieustającej satysfakcji z prowadzenia Łamiblogu. Niech nadchodzący rok przyniesie wiele inspirujących zagadek, błyskotliwych rozwiązań i żywych dyskusji, które – tak jak dotąd – łączą precyzję myślenia z autentyczną pasją.
Życzę Panu , aby każda nowa łamigłówka dawała radość tworzenia, a każda rozwiązana zagadka potwierdzała, że matematyka potrafi być jednocześnie wymagająca, piękna i pełna humoru.
Wszystkiego najlepszego w Nowym Roku! Zbyszek
Dziękuję Panie Zbyszku za życzenia piękne jak matematyka – zwłaszcza rekreacyjna.
Wszystkim łamiblogowiczom – dosiego łamigłówkowego roku.
mp
(66 + 26) * 22 + 2 + 0 = 2026
Wszystkiego dobrego w roku 2026. Liczby w diagramie rzędami od góry: 3, 9, 8; 7, 5, 0; 1, 2, 6, brakuje 4. Najpierw doszedłem do tego, że po prawej stronie trzeba coś pomnożyć przez 0 i dodać 6, potem było trochę zabawy z dopasowywaniem x*y-z = 20.
(6+6)!!! + 60 + 22
To może jeszcze tak: (62 * 66)/2 – 20
2^(2×6-0!)-22