4 na 5
Na jednym z organizowanych w Japonii turniejów dla główkołamaczy pojawiło się w minionym roku eleganckie mnożenie szkieletowe:
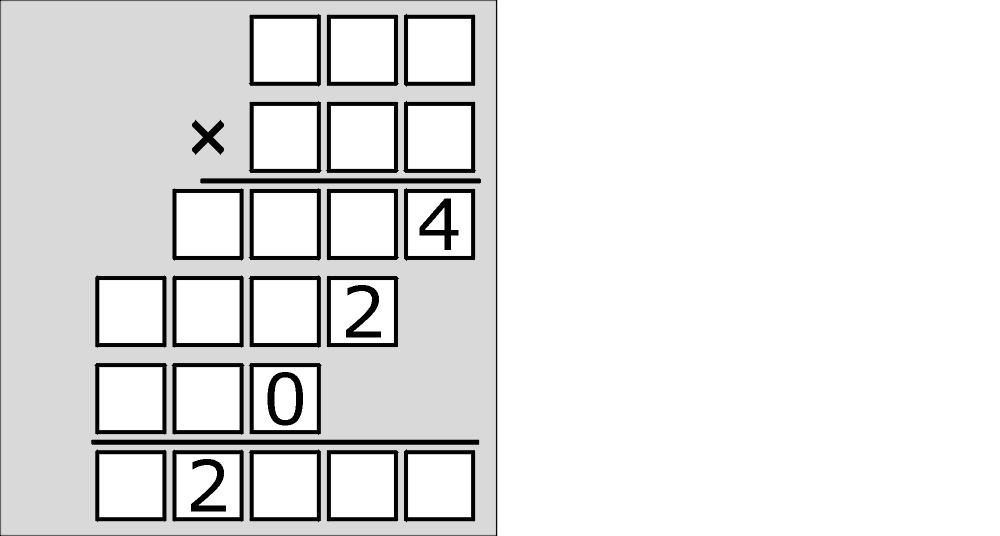
Przypomnę, że celem jest pełna rekonstrukcja działania, czyli wpisanie w puste kratki właściwych cyfr – tak, aby wszystko grało.
Elegancja zadania dotyczy nie tylko formy, czyli ładnie umieszczonego rocznego rządka cyfr, ale także strony merytorycznej – przy rozwiązywaniu podąża się głównie ścieżką logiczną, a udział metody prób i błędów jest niewielki.
Zadanie to podesłali mi ostatnio japońscy koledzy po fachu i zacząłem się zastanawiać, czy jego tegoroczny bliźniak także by się sprawdził, czyli czy miałby rozwiązanie poniższy szkielecik.
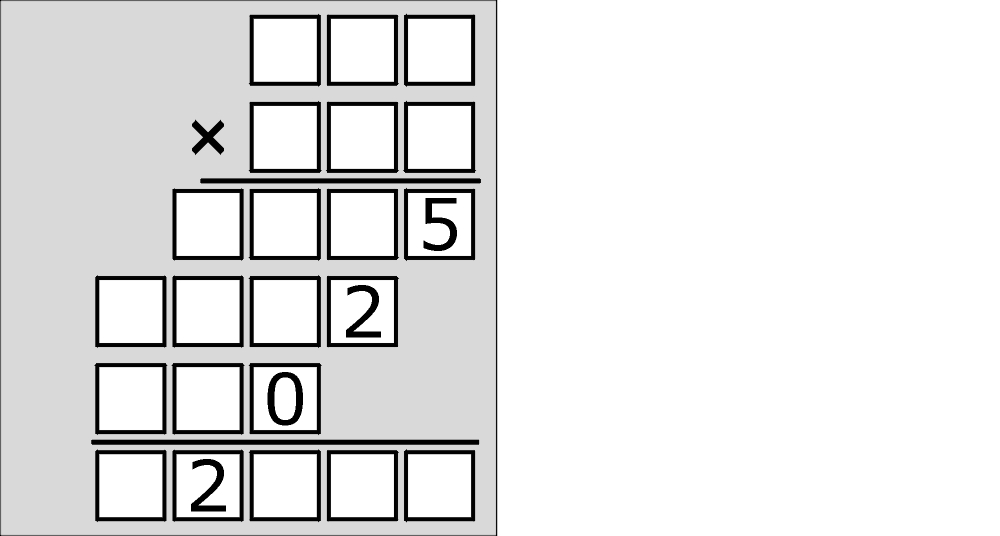
Proszę jak najkrócej udowodnić, że to tegoroczne mnożenie szkieletowe nie ma rozwiązania.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
abc mnożymy przez def.
Z trzeciej linii częściowych iloczynów, której ostatnią cyfrą jest 0, dostajemy c*d=0 (mod 10). Ponieważ d (setki mnożnika) nie może być zerem, jedyną możliwością jest c=5, wtedy d musi być parzyste, bo tylko
c*e=2 (mod 10).
Ale właśnie wykazaliśmy, że c=5. Tymczasem dla każdej cyfry
e mamy 5*e=0 lub 5 (mod 10) nigdy 2. Sprzeczność.
Zatem takie mnożenie szkieletowe nie ma rozwiązania. Znaki = zastępują znaki przystawania.
Z 2024
138 × 598 = 82 524
Po zamianie 5 na 6 są trzy różne rozwiązania.
134×539=72226
162×568=92016
176×526=92576
W sprawie 2025 jest tak:
1) Pierwszy iloczyn cząstkowy kończy się na 5, więc albo mnożna, albo mnożnik musi się kończyć też na 5, natomiast druga z tych liczb musi być nieparzysta.
2) Drugi iloczyn cząstkowy nie kończy się 0 lub 5, więc mnożna nie może kończyć się 5. Wtedy mnożna musi być nieparzysta.
3) Trzeci iloczyn cząstkowy kończy się 0, a to jest możliwe do osiągnięcia tylko wtedy, gdyby mnożna była parzysta lub kończyła się 5.
Te warunki tworzą sprzeczność w określaniu ostatniej cyfry mnożnej.
Najpierw rozwiązałem zadanie drugie, wariant „5”. Oznaczmy mnożenie standardowo ABCxDEF. Jeśli ostatnią cyfrą wyniku mnożenia ABCxF ma być 5, to znaczy, że jedna z liczb C lub F musi być równa 5, a druga – nieparzysta. Jeśli ostatną cyfrą ABCxE ma być 2, to nie może być C=5, czyli musi być F=5. C zatem jest 1, 3, 7, lub 9, jeśli po przemnożeniu przez D ma być 0, to musiałoby D być równe 0, co jest niemożliwe, bo jest to pierwsza cyfra liczby trzycyfrowej. Nie ma zatem takiej szóstki A, B, C, D, E, F, by zapis mnożenia był, jak podano.
W wariancie „4” D nadal nie może być równe 0, więc musi być 5, a C musi być liczbą parzystą. Dodatkowo zarówno E, jak i F, muszą być większe od 5, bo ABCxD jest liczbą tylko trzycyfrową, a ABCxE i ABCxF – czterocyfrowymi.
Ostatnią cyfrą CxF ma być 4, a CxE – 2. C nie może być 0, zostają możliwości 2, 4, 6, 8.
Dla C = 2, F musi być 7, a E – 6, czyli cały mnożnik – 567.
Dla C = 4, F musi być 6, a E – 8, mnożnik 586.
Dla C = 6, F musi być 9, a E – 7, mnożnik 579.
Dla C = 8, F musi być 8, a E – 9, mnożnik 598.
Dla każdego wariantu należy więc znaleźć A i B. Właściwie B, bo A musi być 1, żeby liczba ABCx5 była trzycyfrowa. Jeśli całkowity wynik ma być liczbą tylko pięciocyfrową, a drugą cyfrą ma być 2, to jest tylko jedno rozwiązanie: 138×598 = 82524.
2024 to
138 * 598
2025 się nie da bo
żeby było pierwsze ujawnione 5 to musi być nieparzysta * 5
gdzie nieparzysta jest u góry ze względu na poniższe 2
nieparzyste które dadzą 2 to 1(*2), 3 (*4), 7 (*6), 9(*8)
nie ma w tym zbiorze 5, jedynej nieparzystej dla której istnieje mnożnik żeby dać 0 z kolejnego wiersza
chyba że ostatnia w drugim wierszu (od prawej) cyfra jest 0
wtedy da się
283
*045
2025
Obszar szkieletu: kolumny a,b,c,d,e, wiersze 1,2,3,4,5,6.
e5*e6=5*1, 5*3, 5*5, 5*7, 5*9 (lub odwrotnie). 5=e6 sprawi, że na d3 nie uzyskamy 2, natomiast e6=1, 3, 7, 9 uniemożliwi c2=0.
Tak w żartach
112 * 562 = 62944
124 * 581 = 72044