Dwupak bis
Nowe rodzaje zadań są jak nieszczęścia – zwykle chodzą parami… łatwe-trudne. Podobnie kontynuacją niezbyt trudnego dwupaku sprzed tygodnia jest dzisiejszy dość twardy orzech. Przypominam instrukcję:
W niektóre kratki diagramu należy wpisać liczby tak, aby:
– w każdym wielokącie (w tym przypadku w prostokącie) ograniczonym niebieską linią znalazła się jedna liczba równa wielkości (liczbie kratek) tego wielokąta;
– w każdym żółtym wielokącie (w tym przypadku w prostokącie 1×8) znalazła się dowolna liczba liczb, których suma powinna być równa wielkości tego wielokąta;
– żadne dwie liczby nie znalazły się w sąsiednich kratkach (mających wspólny bok).
Z lewej strony przykład, z prawej zadanie.
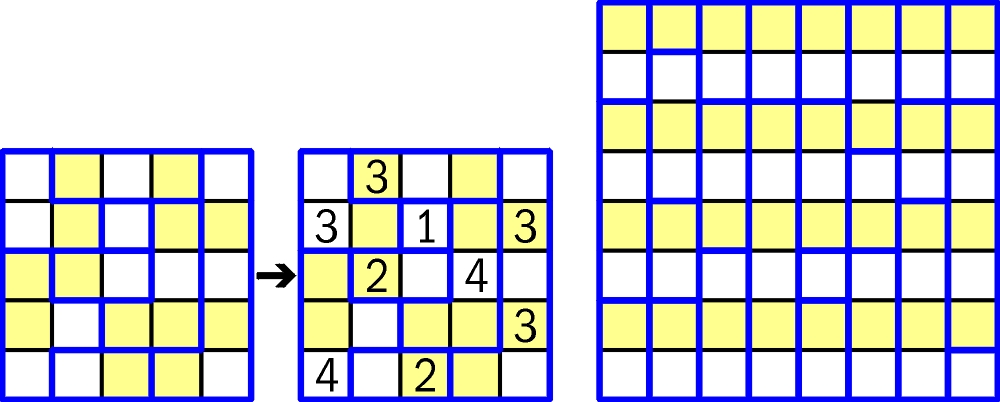
W rozwiązaniu wystarczy podać sumę liczb na obu przekątnych diagramu.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Przekątna od NW = 1, a od NE = 13.
1 2 3 2 2 2 2 2 3 5 4 3 3 2 6 2 2 1 4 2 3 3 2 2 1Logiczne i bardzo łatwe było.
Suma na przekątnych to 14.
Ciekawe czy ktoś w Japonii wymyślił już trzypak z dodatkowymi wielokątami niebieskimi – iloczyn liczb w nich odpowiadałby rozmiarowi wielokąta.
Kto wie – może wtedy byłoby trudniej ?
Suma 1+13=14
R1: · 1 · 2 · 3 · 2
R2: 2 · 2 · 2 · 2 ·
R3: · 3 · · · · · 5
R4: 4 · 3 · 3 · 2 ·
R5: · · · 6 · 2 · ·
R6: · 2 · · 1 · 4 ·
R7: 2 · 3 · · 3 · ·
R8: · 2 · · 2 · · 1
Schemat rozumowania (jak to ugryźć krok po kroku)
Jedynki (1,2), (6,5) i (8,8). Zaznaczamy i skreślamy sąsiadów
Żółte wiersze (1,3,5,7) suma 8.
– W R1 jedyna „3” leży w kol. 6 ⇒ 3 jest wymuszona. Do sumy 8 brakuje 4, które jedynie da się uzyskać jako 2+2 bez sąsiedztwa ⇒ (1,4)=2 i (1,8)=2.
– W kol. 2 klatka 1×3 nie może wziąć „3” w R1 (zajęte przez 1) ani w R2 (sąsiaduje z 1 z R1), więc musi w R3 ⇒ (3,2)=3.
– W R3 dopełnienie do 8 wymusza „5” w jedynym miejscu, gdzie jest dostępna „5” ⇒ (3,8)=5.
Po wpisach z poprzedniej operacji niektóre kolumny zamykają się same (np. kol. 8: 2 u góry, 5 w środku, 1 na dole). Sprawdzając kolumna po kolumnie, gdzie w danej klatce wciąż można wpisać liczbę (często jest to tylko jedno miejsce) wpisujemy kolejne liczby.
Po każdym wpisie skreślamy sąsiednie w górę/dół/lewo/prawo. To szybko redukuje możliwości w pozostałych klatkach, aż pojawiają się kolejne wymuszenia (np. w kol. 4 „6” ląduje w R5, bo inne miejsca blokują wcześniejsze liczby).
Nieco inna logika spowodowana regularnością żółtych obszarów ale trudność taka sama jak w poprzednim zadaniu.
Nie powiedziałbym, że to „dość twardy orzech”, rozwiązanie znalazłem dość szybko. Mam nadzieję, że poprawne 🙂
Na jednej przekątnej mamy tylko liczbę 1.
Na drugiej 6 + 3 + 2 + 2 = 13.
Razem 14.
1 + 13 = 14
wyszło mi 14
Niebiesko-czarny dysonans polega na zlewaniu się linii z powodu zbyt małej różnicy grubości. Teraz i poprzednio przerysowałem kwadrat, pomijając czarne linie.
11